- Hệ thống thông tin địa lý (Geographic Information System - GIS) là
một hệ thống thông tin xử lý dữ liệu không gian-thời gian (gọi
tắt: dữ liệu không gian)
- GIS is a system of computer hardware, software, and people that support the capture, management, analysis, and display of spatial data
- Spatial data: Dữ liệu không gian, hay dữ liệu có thông tin vị trí
- GIS không chỉ xử lý dữ liệu không gian mà còn xử lý dữ liệu phi không gian gắn với các dữ liệu không gian
Hệ thống thông tin địa lý
Phần 1 - Hệ qui chiếu, mốc trắc địa, hệ tọa độ, phép chiếu bản đồ
Nguyễn Hải Châu (nhchau@gmail.com)
Trường Đại học Công nghệ, ĐHQGHN
Định nghĩa hệ thống thông tin địa lý
Các ứng dụng của GIS
- GIS có ứng dụng rất rộng rãi từ cá nhân, cộng đồng; các tổ chức nghiên cứu,
kinh doanh, chính phủ với nhiều phạm vi và qui mô khác nhau.
- Quản lý tội phạm
- Sức khỏe cộng đồng
- Biến đổi và sử dụng đất
- Địa lý lịch sử
- Viễn thám
- Quản lý tài nguyên
- Quản lý chất thải
- Bản đồ
- v.v..
- Tham khảo: https://www.facebook.com/HumanPhysicalGeography/
Tài liệu tham khảo
- Narayan Panigrahi. Computing in Geographical Information System. CRC Press, 2015.
- Otto Huisman and Rolf De By. Principles of Geographic Information Systems: An introductory textbook. The International Institute for Geoinformation Science and Earth Observation, 2009.
- Stephen R. Galati. Geographical information systems demystified. Artech House, 2006.
- I. Heywood, S. Cornelius, S. Carver, An introduction to geographical information systems, 3rd edition, Pearson Education, 2006.
- J. B. Campbell, Introduction to Remote Sensing. New York London: The Guilford Press, 2002
Giới thiệu
- Nội dung bài giảng:
- Giới thiệu về trắc địa và mô hình hóa toán học bề mặt trái đất
- Các hệ qui chiếu
- Mốc trắc địa, các hệ tọa độ và biến đổi hệ tọa độ
- Các phép chiếu bản đồ, đặc tính và ứng dụng
Trắc địa
- Trắc địa (geodesy, hay còn gọi là geodetics) là ngành khoa học nghiên cứu
các phương pháp, kỹ thuật đo đạc một cách chính xác trái đất và các
đối tượng nằm trên trái đất.
- Mô hình hóa hình dạng và kích cỡ trái đất
- Xác định bán kính của trái đất tại một điểm bất kỳ
- Xác định mốc trắc địa
- Có 3 cách đo đạc:
- Đo đạc bằng vật lý
- Đo đạc bằng hình học
- Đo đạc bằng vệ tinh
Các mô hình toán học biểu diễn bề mặt trái đất
Có 3 mô hình thường được các nhà nghiên cứu trong ngành trắc địa sử dụng là:
- Bề mặt vật lý của trái đất
- Tham chiếu geoid
- Tham chiếu ellipsoid
Mô hình vật lý
- Bề mặt vật lý của trái đất: nhấp nhô
- Mô hình hóa bề mặt trái đất theo mô hình vật lý rất khó vì có nhiều ngoại lệ trong các công thức
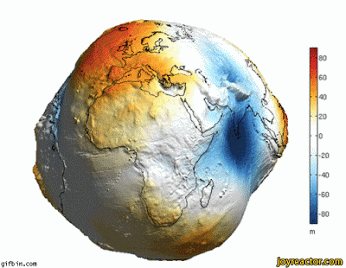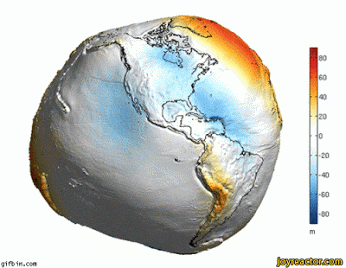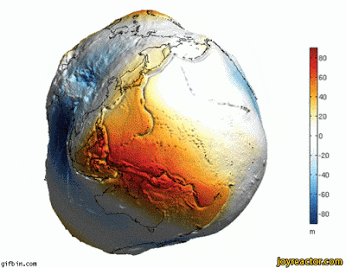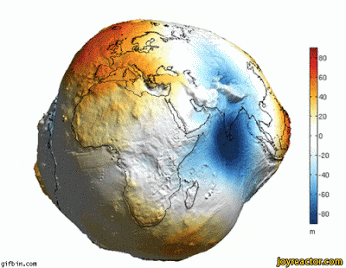
Mô hình geoid
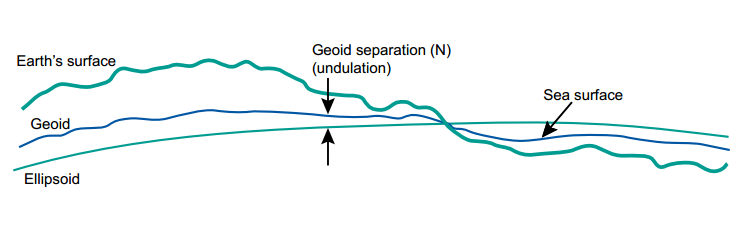
- Mô hình ellipsoid dùng để tham chiếu các tọa độ \((x, y)\) và cũng được dùng để làm bề mặt tham chiếu cho tọa độ \(z\) (cao độ)
- Mô hình geoid dùng để tham chiếu cao độ, chính xác và nhất quán hơn mô hình ellipsoid; geoid không được dùng để tham chiếu tọa độ \((x,y)\)
- geoid có thể hiểu một cách không hình thức là hình dạng bề mặt nước biển dưới sự tác động của lực hấp dẫn, bỏ qua các yếu tố gió và thủy triều
- geoid được định nghĩa là một bề mặt đẳng thế hấp dẫn (equipotential surface: giá trị thế năng
hấp dẫn một hằng số \(\Phi\) trên toàn bộ bề mặt) sao cho bề mặt đó xấp xỉ tốt nhất với mặt biển
ở mức nước biển trung bình toàn cầu.
- Xấp xỉ tốt nhất được hiểu là sai số toàn phương trung bình (root mean square error - RMSE) nhỏ nhất
- Tham khảo: http://www.ngs.noaa.gov/GEOID/geoid_def.html
Mô hình ellipsoid
- Rất "đẹp" về mặt toán học, rất tốt cho việc biểu diễn tọa độ 2 chiều \((x,y)\)
- Được sử dụng rộng rãi
- Khá gần với bề mặt vật lý của trái đất hoặc geoid
- Có hai mô hình ellipsoid phổ biến:
- Mô hình 1: Lựa chọn tâm của ellipsoid trùng với trọng tâm của trái đất. Ellipsoid này được gọi là ellipsoid địa tâm (geocentric), ví dụ: WGS 72, WGS 84, ITRS (International Terrestial Reference System).
- Mô hình 2: Ellipsoid được lựa chọn sao cho phù hợp nhất với mốc trắc địa cục bộ. Ví dụ: Ellipsoid Everest, ellipsoid Bessel.
- Hiện nay có hàng trăm loại ellipsoid ở cả hai mô hình trên đang được sử dụng trên thế giới.
Phương trình toán học của ellipse và ellipsoid
- Phương trình của ellipse: \[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\] trong đó \(a>b\); \(a\) là bán trục lớn và \(b\) là bán trục nhỏ.
- Độ lệch tâm \(e\) của ellipse được xác định qua biểu thức \(b^2=a^2(1-e^2)\), hay \(e=\frac{\sqrt{a^2-b^2}}{a}\), $ 0<e<1 $.
- Một định nghĩa khác của ellipse là quỹ tích của các điểm trên mặt phẳng có tổng khoảng cách đến hai điểm phân biệt \(A, B\) luôn không đổi.
Phương trình toán học của ellipse và ellipsoid
- Phương trình của ellipsoid: \[\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{y^2}{c^2}=1,\] với giả thiết \(a\geq b\geq c\) không làm mất tính tổng quát. Ellipsoid có 3 bán trục: \(a, b, c\).
- Nếu \(a=b>c\), ta có ellipsoid dẹt (oblate ellipsoid).
- Khi một ellipse \(E\) quay quanh bán trục nhỏ, quĩ tích của nó tạo ra ellipsoid dẹt.
- Ellipse \(E\) được gọi là ellipse kinh tuyến. Mặt phẳng chứa ellipse kinh tuyến được gọi là mặt phẳng kinh tuyến (meridian plane).
- Mặt phẳng tạo ra do quĩ tích của bán trục lớn của ellipse \(E\) gọi là mặt phẳng xích đạo (equator plane). Giao của mặt ellipsoid với mặt phẳng xích đạo gọi là đường xích đạo.
- Nếu $ a=b<c$, ta có ellipsoid dài (prolate ellipsoid). Khi một ellipse quay quanh bán trục lớn, quĩ tích của nó tạo ra ellipsoid dài.
- Nếu \(a=b=c\), ta có mặt cầu (sphere)
Minh họa
- Ellipse:
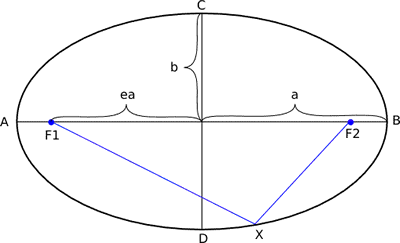
- Ellipsoid dẹt (trái) và dài (phải):
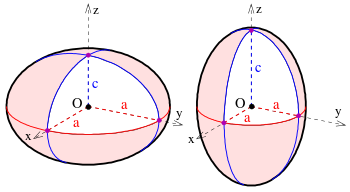
- Trái đất có hình dạng gần giống ellipsoid dẹt với hai cực Bắc, Nam nằm trên bán trục nhỏ.
Các tham số ellipsoid của trái đất
- Trái đất được mô hình hóa là một ellipsoid dẹt (\(a=b>c\)). Trong thực tế người ta không xác định cả hai tham số \(a, b\) mà thường xác định bán trục lớn \(a\) và độ dẹt \(f\):\[f=\frac{a-b}{a}.\]
- Ellipsoid cũng có thể được xác định bằng tham số bán trục lớn \(a\) và độ lệch tâm \(e\): \[e^2=1-\frac{b^2}{a^2}=\frac{a^2-b^2}{b^2}=2f-f^2\]
- Khi biết \(a\) và một trong các tham số \(b\), \(e\) hoặc \(f\), ta có thể tính các tham số còn lại.
- Với trái đất các tham số thường được xác định như sau: \[a=6378135m, b=6356750.52m, f=\frac{1}{298.26}, e=0.08181881066\]
Một số mô hình ellipsoid khác
- Hệ thống tham chiếu trắc địa Ấn Độ IGRS có tính đến núi Everest: \[a=6377301.243m, b=6356100.231m, f=\frac{1}{300.8017}, e=0.08147298\]
- Mô hình quốc tế 1924: \[a=6378388m, b=6356912m, f=\frac{1}{297.000}\]
- Mô hình GRS 1967: \[a=6378169m, b=6356775m, f=\frac{1}{298.247}\]
- Mô hình GRS 1980 và WGS 84: \[a=6378137m, b=6356752m, f=\frac{1}{298.257}\]
Vĩ độ và kinh độ
- Một điểm \(P\) trên ellipsoid có thể được xác định bởi vĩ độ (latitude) và kinh độ (longitude).
- Vĩ độ là góc của mặt phẳng xích đạo với mặt phẳng chứa \(P\) và trục lớn của ellipsoid.
- Kinh độ là góc của mặt phẳng kinh tuyến đi qua \(A\) với mặt phẳng kinh tuyến gốc (tham chiếu).
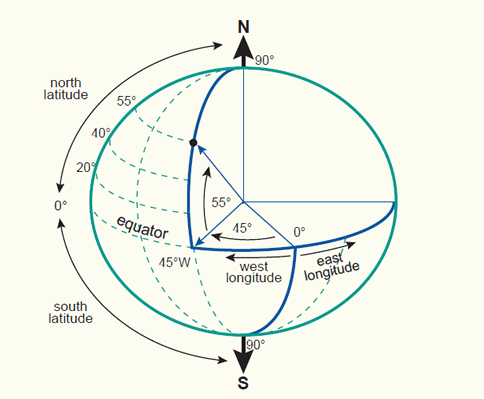
Vĩ độ, kinh độ + cao độ (altitude) \(h\)
Một điểm \(P\) được xác định bởi vĩ độ \(\phi\), kinh độ \(\lambda\), và cao độ \(h\):
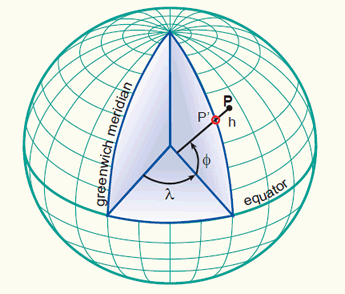
Miền giá trị của vĩ độ và kinh độ
- Vĩ độ có giá trị từ -90 đến 90 độ, kinh độ có giá trị từ -180 đến 180 độ
- Vĩ tuyến (parallel): tập các điểm có vĩ độ bằng nhau, kinh tuyến (meridian): tập các điểm có kinh độ bằng nhau
- Vĩ tuyến 0: đường xích đạo. Kinh tuyến gốc (prime meridian, 0 độ): đi qua đài thiên văn Greenwich, London do Sir George Airy thiết lập vào năm 1851 (xem thêm: https://en.wikipedia.org/wiki/Meridian_circle).
- Tia laser đánh dấu kinh tuyến 0 (theo Airy) tại đài quan trắc Hoàng gia Anh, chiếu
theo hướng Nam-Bắc (https://goo.gl/maps/NNns7ZH8mJq)

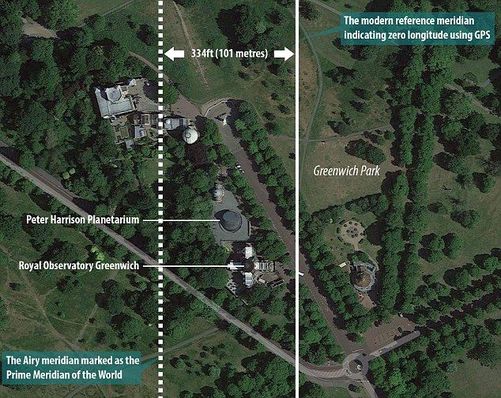
Đánh dấu kinh tuyến gốc tại Greenwich
Sai khác giữa kinh tuyến gốc Airy và số đo GPS
- Các nhà khoa học đã sử dụng thiết bị GPS (Global Positioning System) độ chính xác cao để đo kinh tuyến 0 do Airy xác lập. Kết quả: Kinh tuyến 0 do Airy xác lập bị lệch về phía Tây ~101-102m.

Qui ước cách viết vĩ độ, kinh độ
- Các cách viết kinh độ và vĩ độ:
- Sử dụng hệ thập phân: Trường Đại học Công nghệ: vĩ độ=21.038342, kinh độ=105.782602
- Sử dụng độ/phút/giây: Trường Đại học Công nghệ: vĩ độ=21\(^\circ\) 02'18"N, kinh độ=105\(^{\circ}\) 46'57"E
- Mối quan hệ giữa hai cách viết:
- Vĩ độ dương: N (bắc bán cầu), vĩ độ âm: S (nam bán cầu)
- Kinh độ dương: E (phía đông kinh tuyến gốc), kinh độ âm: W (phía tây kinh tuyến gốc)
Một số tọa độ ở Việt Nam
- Tháp Rùa, Hà Nội: vĩ độ=21.0278497, kinh độ=105.8500824
- Dinh Thống Nhất, TP Hồ Chí Minh: vĩ độ=10.7771283, kinh độ=106.6932683
- Đại Nội, Huế: vĩ độ=16.46843, kinh độ=107.5764285
Các phương pháp xác định vĩ độ
Trong thực tế hình dạng của trái đất rất phức tạp nên việc xác định vĩ độ thực sự là thách thức. Do đó người ta có các phương pháp xác định vĩ độ khác nhau tùy theo ứng dụng:
- Vĩ độ trắc địa (geodetic latitude): Được chấp nhận trên toàn cầu
- Vĩ độ địa tâm (geocentric latitude)
- Vĩ độ cầu (spherical latitude)
- Vĩ độ giảm thiểu (reduced latitude)
- Vĩ độ điều chỉnh (rectifying latitude)
- Vĩ độ authalic
- Vĩ độ bảo giác (conformal latitude)
- Vĩ độ đẳng cự (isometric latitude)
- Vĩ độ thiên văn (astronomic latitude)
Hệ qui chiếu và biến đổi tọa độ
- Trắc địa: Mô hình hóa bề mặt và hình dạng trái đất, hệ qui chiếu xác định quan hệ thứ tự của các đối tượng trên trái đất, bao gồm các đối tượng ở trên bề mặt, dưới biển hoặc trên cao.
- Hệ qui chiếu giúp ta định vị các đối tượng
- Một hệ qui chiếu là một khái niệm toán học nhằm mô hình hóa thế giới thực.
Định nghĩa hệ qui chiếu
- Một hệ qui chiếu được xác định bởi:
- Gốc của hệ qui chiếu
- Các trục, có thể trực giao hoặc không trực giao, được sử dụng làm khung qui chiếu xác định hướng
- Hệ qui chiếu có thể được nhúng vào một hình nào đó như trụ, nón, phẳng...
- Gốc của hệ qui chiếu có thể được lựa chọn là vị trí của một đối tượng như các hành tinh (trái đất, mặt trăng...), một tòa nhà...
- Số chiều của hệ qui chiếu được tính bằng số trục
Phân loại hệ qui chiếu:
- Theo số chiều
- Theo hướng của các trục: trực giao hay không
- Theo cách biểu diễn định lượng: thẳng hay cong
- Theo hướng của hệ qui chiếu: tay trái/tay phải
- Theo diện ảnh hưởng: toàn cầu hay cục bộ
- Theo hình dạng mà hệ qui chiếu được nhúng: phẳng, cầu, nón hay trụ
Mốc trắc địa và hệ tọa độ
- Mốc trắc địa (datum) là nền tảng của một hệ tọa độ (coordinate system).
Mốc trắc địa giúp ta xác định được:
- Gốc tọa độ
- Mặt tham chiếu
- Cao độ của một điểm so với mặt tham chiếu
- Datum là một mặt (surface), được mô hình hóa toán học, nhằm mô tả bề mặt một đối tượng một cách chính xác nhất có thể. Trong trường hợp này, đối tượng đó là trái đất.
- Các hệ tọa độ là đặc tính quan trọng của dữ liệu không gian, giúp chúng ta xác định thứ tự, tìm kiếm, sắp xếp, hiển thị và hiểu được quan hệ không gian của các đối tượng
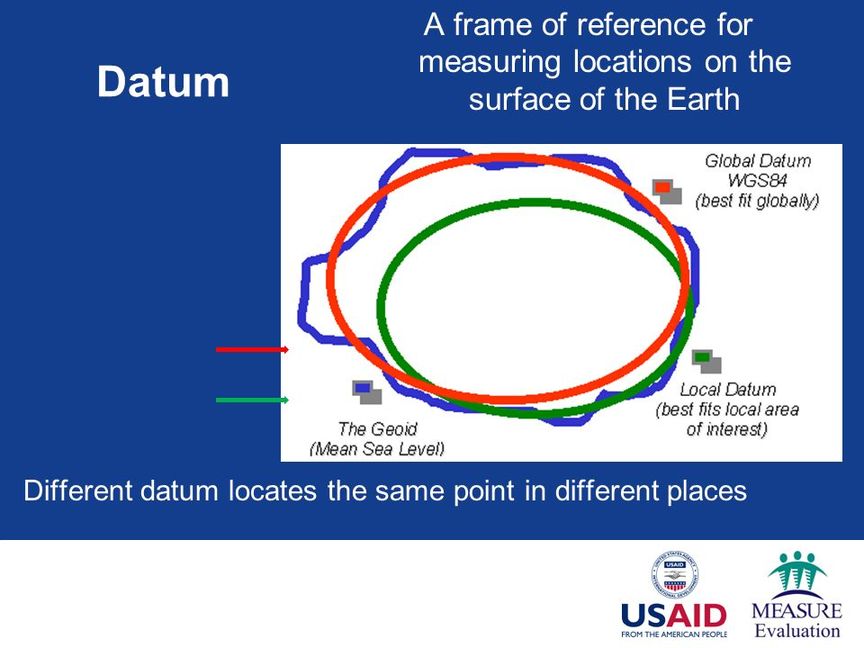
Quan hệ: hệ qui chiếu, datum toàn cầu/cục bộ
Quan hệ: Ellipsoid, geoid và topography
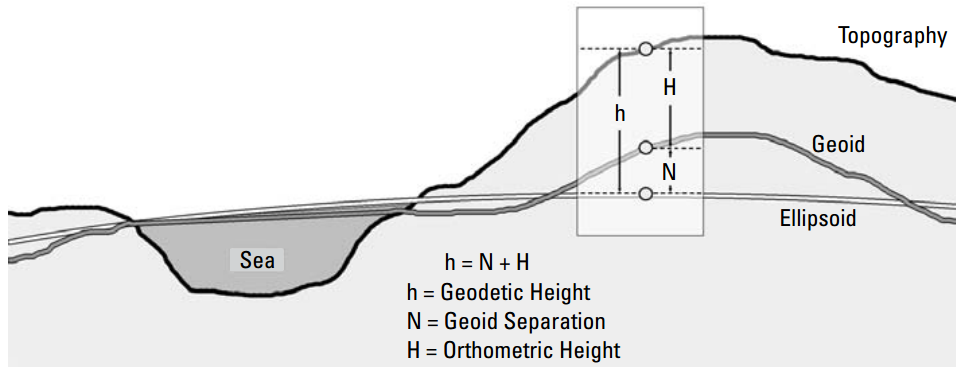
- Thiết bị GPS sử dụng h=geodetic height, orthometric height hoặc ellipsoidal height: cao độ qui chiếu theo ellipsoid
- N còn được gọi là cao độ của geoid (geoid height)
Các hệ tọa độ khác nhau trong GIS
- Có nhiều hệ tọa độ được sử dụng trong GIS với các đặc trưng toán học khác nhau nhằm thỏa mãn các phương thức biểu diễn dữ liệu không gian trong các miền ứng dụng khác nhau
- Trước khi nghiên cứu các hệ tọa độ, chúng ta cần xác định hệ qui chiếu và datum.
- World Geodetic System 1984 (viết tắt WGS 84, WGS 1984 hoặc EPSG:4326) là một bộ chuẩn của
bộ quốc phòng Mỹ công bố năm 1984 bao gồm:
- Hệ qui chiếu toàn cầu (datum hoặc reference ellipsoid)
- Hệ tọa độ
- geoid (hay gravitational equipotential surface - bề mặt đẳng thế hấp dẫn) xác định mức nước biển "tượng trưng"
- WGS 84 được điều chỉnh lần gần nhất vào năm 2004
- Tiền thân của WGS 84: WGS 72, WGS 66, WGS 60
- WGS 84 được sử dụng trong hệ thống định vị toàn cầu GPS
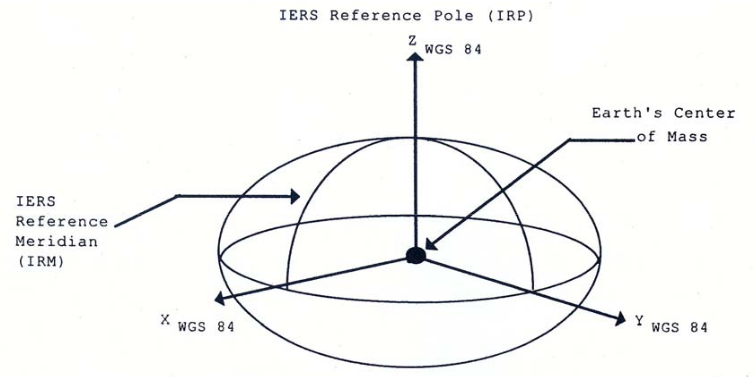
WGS 84
- Gốc tọa độ nằm ở trọng tâm trái đất (sai số ~2cm)
- Kinh tuyến gốc: lệch 102.5m (336.4 ft hoặc 5.31") về phía đông của đài quan trắc Hoàng gia Anh tại Greenwich
- Bề mặt datum của WGS 84 là ellipsoid dẹt, bán trục lớn $a=6,378,137$m, độ dẹt \(f=1/298.257223563\) --> bán trục nhỏ $b=6,356,752.3412$m.
- Ban đầu WGS 84 sử dụng geoid theo EGM84 (Earth Gravitational Model 1984)
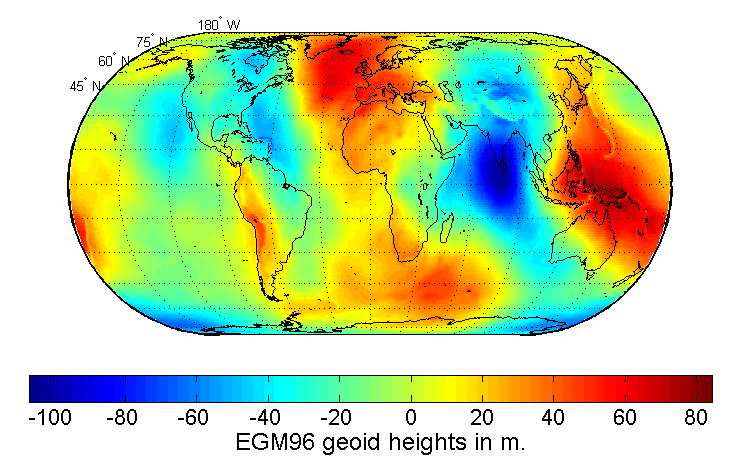
- Từ năm 2004, WGS 84 sử dụng geoid xác định theo EGM96. Độ lệch của EGM96 so với ellipsoid của WGS84 khoảng từ -105m đến 85m. Tham khảo mô hình EMG96 tại https://en.wikipedia.org/wiki/EGM96
- Tham khảo WGS 84: https://www.iho.int/iho_pubs/standard/S60_Ed3Eng.pdf
WGS 84
EMG96
Các hệ tọa độ khác nhau trong GIS
- Hệ tọa độ Descartes (Rectangular Cartesian coordinate system)
- Hệ tọa độ địa lý (Geographic coordinate system)
- Hệ tọa độ cầu (Spherical coordinate system)
- Hệ tọa độ trụ (Cylindrical coodinate system)
- Hệ tọa độ cực và tọa độ cực logarit (Polar and log-polar coordinate system)
- Hệ tọa độ ECEF (Earth centered Earth fixed coordinate system)
- Khung tham chiếu qui chiếu quán tính mặt đất (Inertial terrestial reference frame - ITRF)
- Các khái niệm lưới (grid), UTM, lưới Mercator và lưới GRID quân sự
- Hệ tọa độ vũ trụ (Celestial coordinate system)
Chuyển đổi hệ tọa độ
- Các đối tượng địa lý được biểu diễn khác nhau trong các hệ tọa độ khác nhau nhằm phục các mục đích ứng dụng đa dạng
- Khi có nhiều mục đích ứng dụng, cần chuyển đổi tọa độ của một đối tượng từ hệ tọa độ này sang hệ tọa độ khác bằng các toán tử
- Khi chuyển đổi hệ tọa độ, ta cần xem xét các yếu tố:
- Datum
- Phương pháp chuyển đổi tọa độ
Chuyển đổi datum
- Trái đất liên tục biến đổi do nhiều yếu tố (động đất, núi lửa, sóng thần, tự quay quanh trục...) do đó trọng tâm thay đổi theo thời gian --> thay đổi geoid, mức nước biển trung bình...
- Thực tế: Datum thay đổi theo thời gian, cần được cập nhật thường xuyên
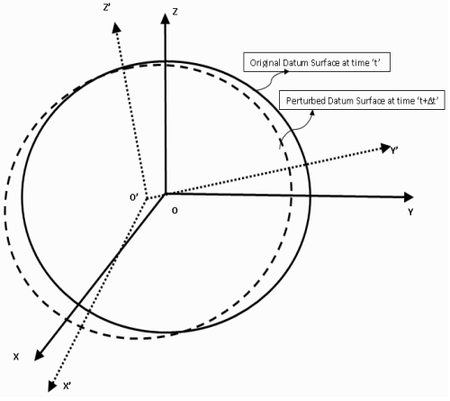
Chuyển đổi tọa độ hai chiều (2D)
Các phép chuyển đổi (biến đổi) tọa độ 2D thường dùng bao gồm:
- Tọa độ Descartes sang tọa độ cực
- Tọa độ Descartes sang tọa độ cực logarit
- Tọa độ Descartes sang tọa độ song cực (bipolar)
Chuyển đổi tọa độ ba chiều (3D)
Các phép biến đổi tọa độ 3D thường dùng:
- Tọa độ cầu sang tọa độ Descartes 3D
- Tọa độ trụ sang tọa độ Descartes 3D
- Tọa độ Descartes 3D sang tọa độ cầu
Các phép chiếu bản đồ
- Chúng ta đã xem xét: Trắc địa --> Mô hình hóa trái đất --> Hệ qui chiếu --> datum/hệ tọa độ
- Để tạo bản đồ (trên mặt phẳng 2 chiều) cần có các phép chiếu bản đồ
- Một phép chiếu bản đồ là một ánh xạ một điểm \(A=(\phi,\lambda)\) trên mặt ellipsoid biểu diễn bề mặt trái đất sang điểm \(A'=(x,y)\) trên một mặt phẳng: \[f(\phi,\lambda)=(x,y)\]
- Ánh xạ ngược \(f^{-1}\) xác định tọa độ địa lý của điểm \(A\) từ tọa độ \((x,y)\) của \(A'\): \[f^{-1}(x,y)=(\phi,\lambda)\]
Các phép chiếu bản đồ thông dụng
- Mặt chiếu tiếp diện với ellipsoid:
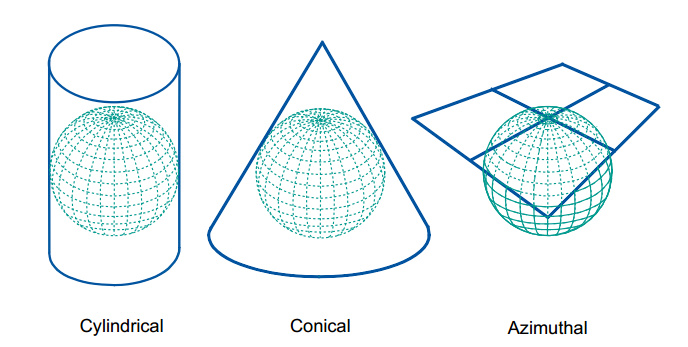
Các phép chiếu bản đồ thông dụng
Mặt chiếu cắt ellipsoid:
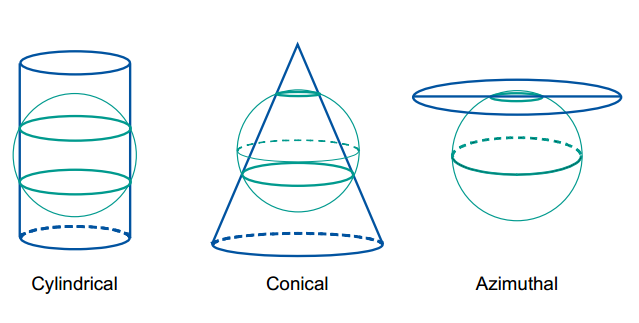
Các phép chiếu bản đồ thông dụng
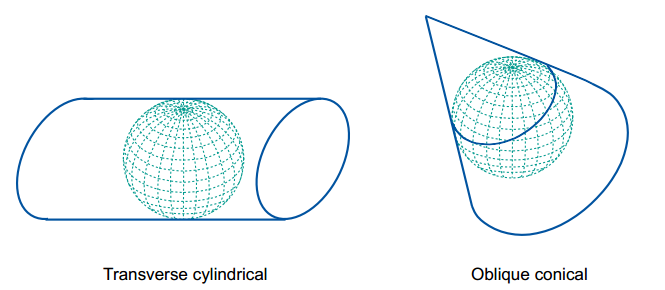
Minh họa các phép chiếu bản đồ thông dụng
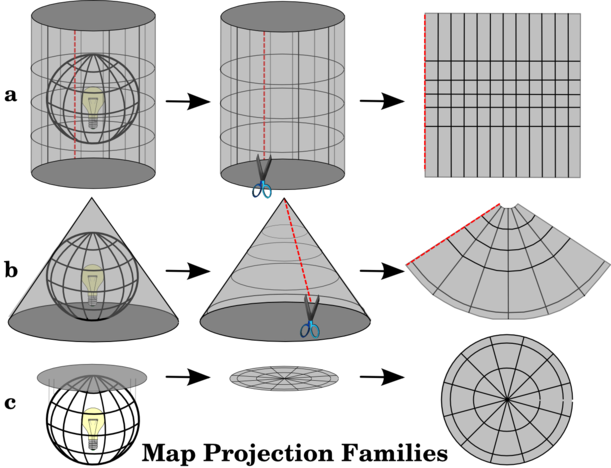
Minh họa các phép chiếu bản đồ thông dụng
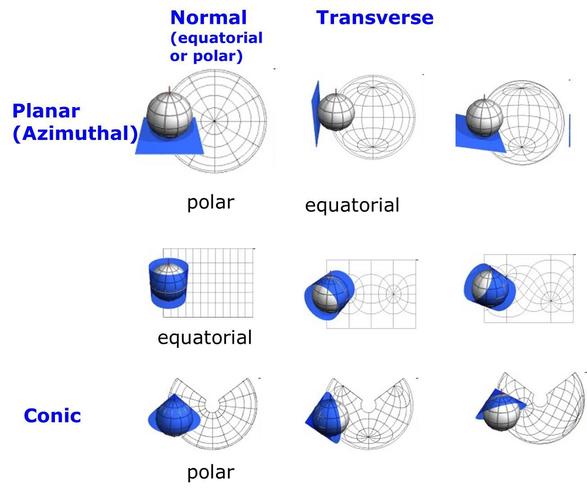
Phép chiếu Mercator (Mercator projection)
- Phép chiếu Mercator là một phép chiếu trụ do nhà bản đồ học người Flemming tên là Gerardus Mercator (1512-1594) phát minh năm 1569.

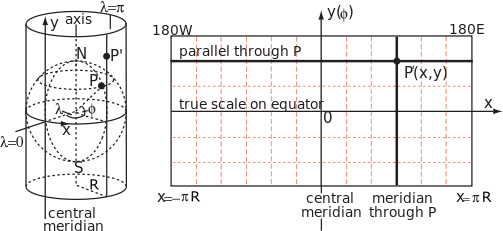
Phép chiếu Mercator
- Bản đồ thế giới từ vĩ độ 82S đến 82N (hoặc từ vĩ độ -82.0 đến 82.0): Lưu ý sự không tuyến tính của vĩ độ trên hình
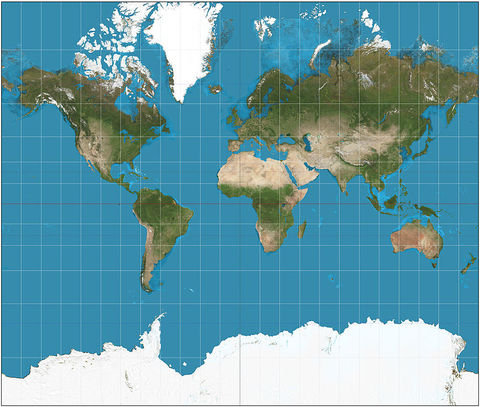
Thay đổi diện tích trong phép chiếu Mercator
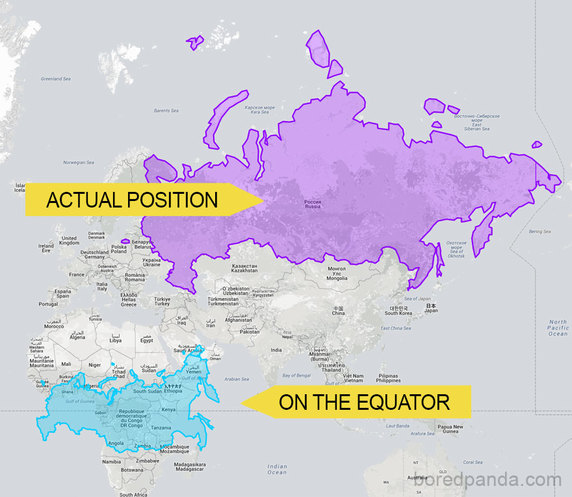
Công thức toán học của phép chiếu Mercator
- Chúng ta xem xét trường hợp đơn giản của phép chiếu Mercator khi xem trái đất có hình cầu. Trường hợp ellipsoid có công thức phức tạp hơn, xem thêm tại https://en.wikipedia.org/wiki/Mercator_projection
- Ánh xạ \(f\) của phép chiếu Mercator: \[x=R(\lambda-\lambda_0), y=R(\ln(\tan(\frac{\pi}{4}+\frac{\phi}{2})))\]
- Ánh xạ \(f^{-1}\): \[\phi=\frac{\pi}{2}-2\arctan(e^{\frac{-y}{R}}), \lambda=\frac{x}{R}+\lambda_0\]
- \(R\) là bán kính hình cầu ở tỷ lệ bản đồ cần vẽ, \(\lambda_0\) là kinh tuyến chuẩn của phép chiếu (thường chọn là kinh tuyến 0)
- Tỷ lệ bản đồ là tỷ số khoảng cách trên bản đồ đó với khoảng cách trên thực địa. Ví dụ bản đồ tỷ lệ 1:500,000 cho biết: 1cm trên bản đồ tương đương 500,000cm=5km trên thực địa.
Định tính tỷ lệ bản đồ
- Tỷ lệ lớn: 1:0 - 1:600,000. Ví dụ: tỷ lệ 1:0.00001 dành cho bản đồ virus, tỷ lệ 1:5000 cho bản đồ đường phố
- Tỷ lệ trung bình: 1:600,000 - 1:2,000,000 dành cho bản đồ quốc gia
- Tỷ lệ nhỏ: 1:2,000,000 - 1:\(+\infty\) dành cho bản đồ thế giới, bản đồ các thiên hà
Tính chất và ứng dụng của các phép chiếu bản đồ
- Phép chiếu trụ (cylindrical): bảo giác (giữ nguyên giá trị góc), thường dùng để xác định phương hướng trong hàng hải, ánh xạ địa hình
- Phép chiếu trụ ngang, ví dụ Mercator ngang (UTM - Universal Transverse Mercator), bảo toàn khoảng cách. UTM được Liên hiệp quốc khuyến cáo từ 1952 cho ánh xạ địa hình
- Phép chiếu Mercator ngang cũng được khuyến cáo cho các bản đồ cục bộ có tỷ lệ cao, ví dụ bản đồ Pan-Europe tỷ lệ 1:500 000
- Phép chiếu nón (conical) bảo toàn tỷ lệ trên tất cả các kinh tuyến. Nước Nga và châu Âu được cho rằng nên sử dụng bản đồ phép chiếu nón.
- Phép chiếu phương vị (azimuthal): Bảo toàn phương vị (hoặc hướng chính xác) tính từ tâm bản đồ
- Phép chiếu phương vị chéo được sử dụng trong bản đồ biển Thái Bình Dương, phép chiếu phương vị bảo toàn diện tích được dùng trong bản đồ thám hiểm hai cực Bắc, Nam
Spatial Reference Identification (SRID)
- SRID là một giá trị nguyên dương dùng để phân biệt các hệ qui chiếu, phép chiếu và hệ tọa độ
- Các công ty, nhà sản xuất có liên quan đến địa lý, không gian đều tự tạo ra SRID của riêng mình hoặc tham chiếu SRID được xác định từ một đơn vị có thẩm quyền, chẳng hạn European Petrolium Survey Group (EPSG)
- Từ năm 2005, Ủy ban khảo sát và định vị của OGP (Oil and Gas Producers) quản lý SRID thay cho EPSG
- WGS 84 được tham chiếu bằng SRID 4326 hoặc EPSG:4326
- Google Maps: SRID 3857 hoặc SRID 900913
- Việt Nam:
- Hệ tọa độ quốc gia VN-2000
- SRID 3405, SRID 3406 và SRID 4756
- Tham khảo: http://spatialreference.org
Tổng kết
Tổng kết
- Mô hình hóa trái đất bằng ellipsoid dẹt
- Tham số ellipsoid có thể thay đổi theo yêu cầu ứng dụng
- Ellipsoid dùng để xác định tọa độ \(x, y\) hoặc \(z\)
- Datum là mốc trắc địa, dùng để xác định tọa độ \(z\)
- Có nhiều hệ tọa độ khác nhau được sử dụng trong GIS --> Chuyển đổi hệ tọa độ
- Các phép chiếu dùng để thể hiện bề mặt 3 chiều của trái đất lên mặt phẳng 2 chiều
- Các hệ qui chiếu có mã định danh SRID; EPSG, sau đó OGP (từ 2005), quản lý các mã định danh này